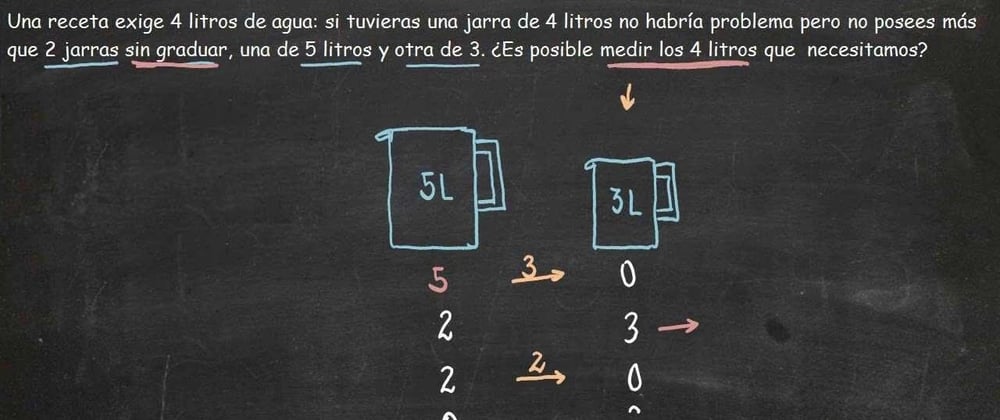
Al empezar a aprender Prolog, surgen ejercicios de razonamiento como el acertijo de las jarras de agua, el cual menciona que se tiene 2 jarras, de 5 y 3 litros de capacidad respectivamente, sin ninguna marca de medición, además se tiene una fuente de agua ilimitada que permite llenar las jarras de agua. Se requiere exactamente 4 litros de agua en una de las jarras. En este blog se explica la resolución del acertijo.
Hay que tener en cuenta 3 aspectos fundamentales antes de programar el acertijo en cualquier lenguaje de programación; y estos son los siguientes:
1. Es necesario entender el problema.
2. Resolver el problema, esto se lo puede hacer mentalmente o como yo, que prefiero plasmar la resolución sobre una hoja de papel, mediante gráficos que ayuden a entender mejor la resolución del acertijo.
3. Por último, una vez que haya resuelto el acertijo o problema, es momento de plasmar la solución utilizando un lenguaje de prgramación, Prolog en este caso.
Para resolver este acertijo se va a utilizar los 3 aspectos recomendados en el punto anterior.
1. ¿Cuál es el problema?
No se puede medir exactamente los 4 litros de agua dado que se dispone de 2 jarras de 5 y 3 litros sin marcas de medición.
2. ¿Cómo resuelvo el problema?
Para lograr medir los 4 litros necesarios, se requiere realizar un conjunto de pasos, veamos:
Se puede partir llenando cualquiera de las 2 jarras, la jarra grande (5lt) o jarra pequeña (3lt), por ejemplo, se llena primero la jarra grande.
Una vez lleno la jarra de 5 litros, se vierte el contenido de la jarra grande en la pequeña, dando como resultado, 2 y 3 litros de agua; la jarra pequeña queda llena.
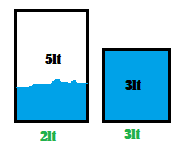
Como tercer paso, se vacía la jarra pequeña.
En el cuarto paso, se vierte el contenido de la jarra grande donde hay 2lt de agua a la jarra pequeña, quedando al final 0 litros de agua en la jarra grande y 2 litros en la jarra pequeña.
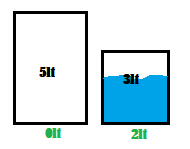
En el quinto paso, se llena nuevamente la jarra grande.
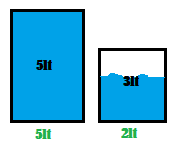
En el paso 6, que es el último, se vierte el contenido de la jarra grande a la pequeña donde hay 2lt de agua, dado que solo falta un litro para llenar la jarra pequeña; y la jarra grande contiene 5 litros de agua, al pasar de la jarra grande a la pequeña, resulta 4 litros de agua en la jarra grande.
En este paso se ha resuelto el problema en 6 pasos, cabe mencionar que esta no es la única solución, dado que existen varias soluciones, por ejemplo, se puede partir llenando la jarra pequeña (3lt).
3. Programar solución
En este punto esta claro lo que se va a programar, el objetivo de este tutorial no es enseñar cómo funciona Prolog, al contrario se entiende que el lector tiene conocimientos, al menos básicos sobre este lenguaje de programación lógico e interpretado.
Se parte de un hecho, donde el estado deseado es que la jarra grande (5lt) contenga 4 litros de agua como estado final, para lo cual en Prolog se representa de la siguiete manera:
estado(4, _ )
Donde, el número 4 representa la cantidad de agua en la jarra grande y el símbolo ( _ ) representa que no interesa el valor en la jarra pequeña (3lt), este estado final se lo representará como el siguiente hecho:
meta(estado(4, _ )).
Para continuar, es necesario definir las variables con las que se va a trabajar, por tanto, a continuación se define las siguientes variables:
CJG = cantidad de agua en la jarra grande
CJP = cantidad de agua en la jarra pequeña
MJG = capacidad máxima de la jarra grande (5lt)
MJP = capacidad máxima de la jarra pequeña (3lt)
A continuación es necesario definir todas las reglas (8 reglas) para la resolución del acertijo, donde la verdad de un hecho depende de la verdad de otro hecho o conjunto de hechos. Un estado posible dependerá de un conjunto de reglas, por ejemplo:
1. El estado posible puede ser que la jarra grande quede llena, y este hecho se representa de la siguiente manera en Prolog:
posible(estado(CJG , CJP), estado(CJG1, CJP), MJG, _)
Dado que las reglas se componen de una cabeza y un cuerpo, falta definir el cuerpo de esta regla, que es nada más que otro conjunto de hechos. Para el posible estado mencionado anteriormente se define ciertas condiciones y estas son: CJG >= 0, CJG < MJG, CJG1 is MJG, el símbolo ( , ) representa un AND en prolog y el ( . ) el final de un predicado, la palabra reservada is representa la igualdad ( = ), por tanto, la regla completa queda de la siguiente manera:
posible(estado(CJG, CJP), estado(CJG1, CJP), MJG, _) :- CJG >= 0, CJG < MJG, CJG1 is MJG .
Esta expresión se lee de la siguiente manera, solo se puede llenar la jarra grande, si la jarra no esta llena. Es decir la jarra grande debe estar vacía o contener una cantidad de agua menor a la capacidad de la jarra (CJG >= 0, CJG < MJG), si esto se cumple la cantidad de agua es actualizada con la capacidad de la jarra lo que equivale a llenar la jarra (CJG1 is MJG).
En el estado posible, se definen 2 estados, esto quiere decir que hay un estado inicial y un final, se puede apreciar también que en el segundo estado cambia CJG por CJG1 dado que solo cambiará de estado la jarra grande. Además el posible estado, recibe 2 argumentos más, que son las capacidades de las jarras, dado que solo me interesa el cambio de estado de la jarra grande, se requiere saber la capacidad de dicha jarra, por tanto paso MJG y dado que no me interesa el estado de la jarra pequeña utilizo el símbolo ( _ ).
2. Otro estado posible a tomar en cuenta, es cuando se llena la jarra pequeña; y esta regla se define de la siguiente manera:
posible(estado(CJG, CJP), estado(CJG, CJP1), _ , MJP):- CJP >= 0, CJP < MJP, CJP1 is MJP.
La explicación de este predicado es similiar a lo explicado anteriromente cuando se llenó la jarra grande.
3 y 4. Los siguientes estados posibles son, cuando se vacían las jarras. Sólo se puede vaciar una de las jarras si esta contiene agua y para vaciar no se requiere saber la capacidad de las jarras.
posible(estado(CJG, CJP), estado(CJG1, CJP), _ , _ ):- CJG > 0, CJG1 is 0.
posible(estado(CJG, CJP), estado(CJG, CJP1), _ , _ ):- CJP > 0, CJP1 is 0.
5 y 6. Aún quedan 2 posibles estados más, estos son cuando se vierte el agua de la jarra grande en la pequeña y la cantidad de agua de la jarra grande es menor o mayor a la cantidad de agua faltante para llenar la jarra pequeña, esta se define así:
posible(estado(CJG, CJP), estado(CJG1, CJP1), _ , MJP):- CJG > 0, CJP < MJP, CJG =< (MJP - CJP), CJG1 is 0, CJP1 is CJP + CJG.
posible(estado(CJG, CJP), estado(CJG1, CJP1), _ , MJP):- CJG > 0, CJP < MJP, CJG > (MJP - CJP), CJG1 is CJG - (MJP - CJP), CJP1 is MJP.
En el predicado anterior se aprecia que cambian los estados de las 2 jarras, ya que al pasar agua de una jarra hacia el otro, los dos estados se ven afectados, por eso la expresión estado(CJG, CJP), estado(CJG1, CJP1), y dado que se se pasa agua desde el recipiente grande a la pequeña es necesario saber la capacidad de la jarra pequeña (MJP), como la capacidad de la jarra grande no me interesa en estos 2 casos utilizo el símbolo ( _ ).
Al pasar agua de la jarra grande a la pequeña hay que tener en cuenta 2 posibles casos, estas son cuando la cantidad de agua a pasar es menor, igual (CJG =< (MJP - CJP)) o mayor (CJG > (MJP - CJP)) a la cantidad de agua faltante para llenar la jarra pequeña.
En el primer caso, la jarra grande queda vacía (CJG1 is 0) y la jarra pequeña queda con la cantidad de agua que ya tenía más la cantidad que se vierte desde la jarra grande (CJP1 is CJP + CJG).
En el segundo caso, la jarra grande queda con la cantidad de agua que tenía inicialmente menos la cantidad de agua faltante para llenar la jarra pequeña (CJG - (MJP - CJP)), lo cual significa que la jarra pequeña queda llena.
Todo esto se cumple si la jarra grande no esta vacía (CJG > 0).
7 y 8. Las 2 últimas reglas a definir son cuando se vierte agua de la jarra pequeña en la grande y la cantidad de agua de la jarra pequeña es menor, igual o mayor a la cantidad de agua faltante para llenar la jarra grande (similar a las reglas 5 y 6), esta se define así:
posible(estado(CJG, CJP), estado(CJG1, CJP1), MJG, _ ):- CJP > 0, CJG < MJG, CJP =< (MJG - CJG), CJP1 is 0, CJG1 is CJG + CJP .
posible(estado(CJG, CJP), estado(CJG1, CJP1), MJG, _ ):- CJP > 0, CJG < MJG, CJP > (MJG - CJG), CJP1 is CJP - (MJG - CJG), CJG1 is MJG.
La explicación de la 2 expresiones anteriores son similares a las reglas 5 y 6, con la diferencia, de que es necesario saber la capacidad del recipiente grande (MJG) para determinar la cantidad de agua faltante en dicho recipiente.
Lista de estados
La solución al acertijo es una lista de estados (los que fueron analizados anteriormente) y es conveniente determinar que no existan estados repetidos, por tanto hay que verificar si un elemento pertenece a una lista, en Prolog se define de la siguiente manera:
miembro(X, [X | _ ]).
miembro(X, [ _ | L ]) :- miembro(X, L).
Solución
A continuación, se define la solución a este acertijo:
E = cabeza de la lista L = cola de la lista
solucion([E | L], [E | L], MJG, MJP) :- meta(E).
El predicado anterior, la solución base (definida con el mismo nombre sin acento) recibe 4 parámetros, los 2 primeros valores son listas y deben ser iguales ([E | L], [E | L]), mismas que se dividen en cabeza y cola ([E | L]), los 2 últimos valores son la capacidad de las jarras. En resúmen, hay solución, si es la meta que estoy buscando; la meta recibe la cabeza de la lista el cual es un estado y anteriormente ya se definió el hecho de la meta deseada para que sea solución meta(estado(4, _ )), en el caso que la solución base no se cumpla se define lo siguiente:
solucion([E | L], LS, MJG, MJP) :- posible(E, EP, MJG, MJP), not(miembro(EP, L)), solucion([EP, E | L], LS, MJG, MJP).
El predicado anterior define otra regla que obtiene la lista de estados posibles hasta llegar a la solución base, la solución recibe 4 valores, los 2 primero valores son listas, la primera lista es la lista de estados posibles (dividido en cabeza y cola) y la misma será almacenada en la segunda lista que es la lista solución ([E | L], LS).
En el cuerpo de la regla se verifica que a partir del último estado posible (cabeza de la lista) exista un nuevo estado posible posible(E, EP, MJG, MJP), además el nuevo estado posible no debe estar repetido en la lista de estados posibles not(miembro(EP, L)), en cuanto se cumpla estas 2 condiciones se llama una vez más al predicado solucion, pero en esta ocación se agrega el nuevo estado a la lista de estados ([EP, E | L]), esto se repetirá hasta que se encuentre la meta.
Para ejecutar el programa en SWI-Prolog, se lo hace de la siguiente manera:
solucion([estado(0, 0)], L, 5, 3).
Al predicado solución se le envía la lista de estados, va empezar solo con un elemento ([estado(0, 0)]) en la lista de estados posibles, la variable donde se almacenarán dichos estados (L) y la capacidad de la jarra grande (5) y pequeña (3) respectivamente.
La salida es la siguiente (se mostrarán varias listas de diferentes soluciones):
L = [estado(4, 0), estado(1, 3), estado(1, 0), estado(0, 1), estado(5, 1), estado(3, 3), estado(3, 0), estado(0, 3), estado(..., ...)|...] ;
L = [estado(4, 3), estado(4, 0), estado(1, 3), estado(1, 0), estado(0, 1), estado(5, 1), estado(3, 3), estado(3, 0), estado(..., ...)|...] ;
L = [estado(4, 3), estado(5, 2), estado(0, 2), estado(2, 0), estado(2, 3), estado(5, 0), estado(0, 0)] ;
...
A continuación se muestra todo el código:
meta(estado(4, _ )) .
posible(estado(CJG, CJP), estado(CJG1, CJP), MJG, _) :- CJG >= 0, CJG < MJG, CJG1 is MJG .
posible(estado(CJG, CJP), estado(CJG, CJP1), _ , MJP):- CJP >= 0, CJP < MJP, CJP1 is MJP.
posible(estado(CJG, CJP), estado(CJG1, CJP), _ , _ ):- CJG > 0, CJG1 is 0.
posible(estado(CJG, CJP), estado(CJG, CJP1), _ , _ ):- CJP > 0, CJP1 is 0.
posible(estado(CJG, CJP), estado(CJG1, CJP1), _ , MJP):- CJG > 0, CJP < MJP, CJG =< (MJP - CJP), CJG1 is 0, CJP1 is CJP + CJG.
posible(estado(CJG, CJP), estado(CJG1, CJP1), _ , MJP):- CJG > 0, CJP < MJP, CJG > (MJP - CJP), CJG1 is CJG - (MJP - CJP), CJP1 is MJP.
posible(estado(CJG, CJP), estado(CJG1, CJP1), MJG, _ ):- CJP > 0, CJG < MJG, CJP =< (MJG - CJG), CJP1 is 0, CJG1 is CJG + CJP .
posible(estado(CJG, CJP), estado(CJG1, CJP1), MJG, _ ):- CJP > 0, CJG < MJG, CJP > (MJG - CJG), CJP1 is CJP - (MJG - CJG), CJG1 is MJG.
/* Verifica si un elemento pertenece a una lista */
miembro(X, [X | _ ]).
miembro(X, [ _ | L ]) :- miembro(X, L).
/* Implementando solución */
solucion([E | L], [E | L], MJG, MJP) :- meta(E).
solucion([E | L], LS, MJG, MJP) :- posible(E, EP, MJG, MJP), not(miembro(EP, L)), solucion([EP, E | L], LS, MJG, MJP).
También pueden encontrar el mismo código en GitHub.
Con esto concluimos, espero haber ayudado a entender mejor, la resolución del problema en Prolog, si tienen alguna pregunta no duden en escribirme.
¡Gracias por su lectura!